齒輪各部位的名稱
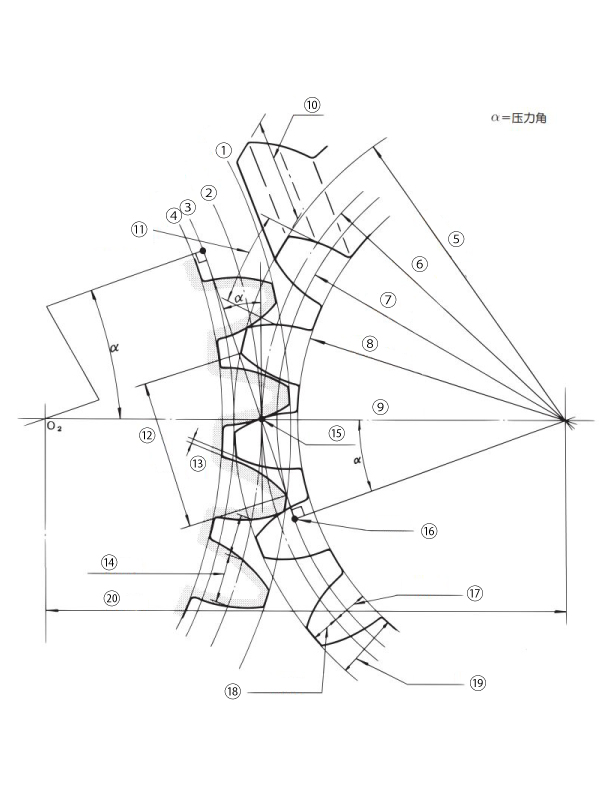
- 齒頂圓
- 分度圓
- 基圓
- 齒根圓
- 齒頂圓直徑
- 分度圓直徑
- 基圓直徑
- 齒根圓直徑
- 中心線
- 齒寬
- 周節(分度圓齒距)
- 嚙合長度
- 齒隙
- 弧齒厚
- 節點
- 干涉點
- 齒根高
- 齒頂高
- 全齒高
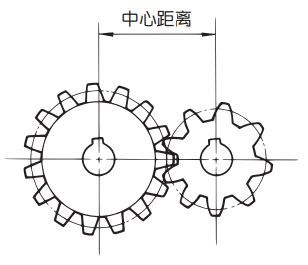
- 中心距離
表示輪齒大小的是 《模數》
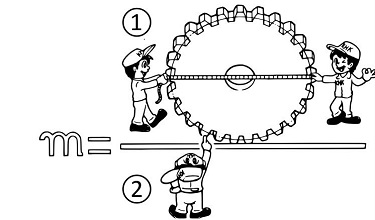
- 分度圓直徑
- 齒數
如上所述,輪齒的大小由模數來決定。
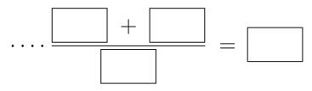
用公式來表示為 : m = d / z ( 模數 = 分度圓直徑 / 齒數 )
與模數的關系如下所示。
分度圓直徑 : d = mz ( 分度圓直徑 = 模數 × 齒數 )
齒數 : z = d / m ( 齒數 = 分度圓直徑 / 模數 )
齒距 : p = πm ( 齒距 = π × 模數 )
齒距是????????
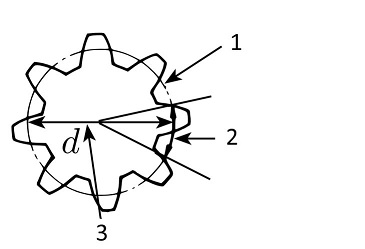
1. 周長 = πd
2. 齒距 = 周長 / 齒數 = πd / z
3. 直徑 = d
周長除以齒數的商是齒距的長度。也就是說 :
( 齒距 = 周長 (πd) / 齒數 (z) )
那么,分度圓是??????
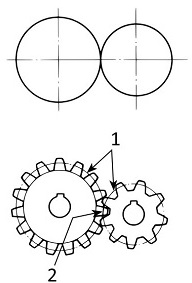
1. 摩擦輪 (分度圓)
2. 兩個分度圓必須相切
這是摩抆輪,施加的外力過大會產生滑動,達不到理想的傳動效果。
所以,人們在摩抆輪的外周上作了一些突起,讓這些突起相互嚙合旋轉,這就是齒輪。
摩抆輪的外周作為分度圓,兩個齒輪的分度圓一定要相切。
總結
- 輪齒的大小用模數來表示。
- 為了使齒輪相互嚙合,兩個齒輪的法向基圓齒距必須相等。
習題
直齒輪
模數 m = 3, 小齒輪齒數 z1 = 15, 大齒輪齒數 z2 = 55
- 分度圓直徑
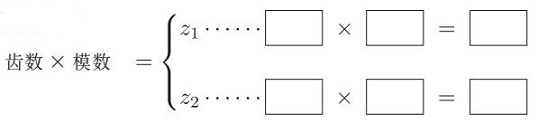
- 齒頂圓直徑

- 中心距離

斜齒齒輪
模數 m = 3, 小齒輪齒數 z1 = 15, 大齒輪齒數 z2 = 55, 螺旋角 β0 = 16o15′, cosβ0 = 0.96
- 分度圓直徑
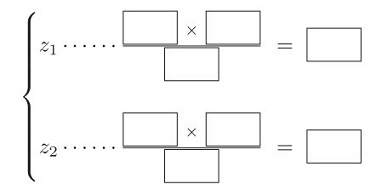
- 齒頂圓直徑
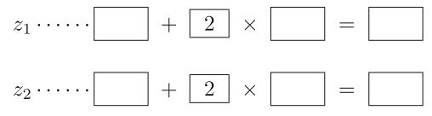
- 中心距離